4 I NUMERI NEGATIVI E REALI NEL SISTEMA BINARIO
4 I NUMERI NEGATIVI E REALI NEL SISTEMA BINARIO
La rappresentazione in modulo e segno
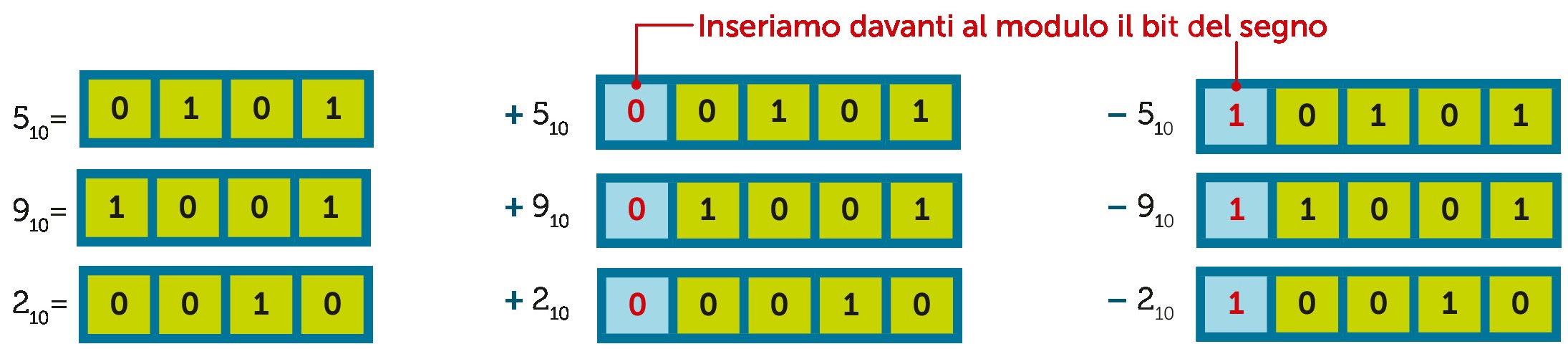
Nel metodo modulo e segno (MS) al numero binario viene anteposto un bit che, per convenzione, assume il valore:
- 0 se il numero è positivo;
- 1 se il numero è negativo.
Per esempio il numero 510, che in base 2 si scrive 1012, in modulo e segno avrà le due rappresentazioni:
0101MS per indicare + 5 e 1101MS per indicare – 5
In matematica il concetto, risulta piuttosto semplice da applicare: si scrive il valore assoluto (modulo) del numero (per esempio 1012) e davanti si inserisce un bit che rappresenta il suo segno. Se il valore assoluto ha più di tre di cifre è sufficiente inserire il bit che rappresenta il segno “un po’ prima” della cifra più a sinistra.
In informatica il criterio “un po’ prima” è inapplicabile perché il computer non è in grado di ragionare come un matematico. Occorre trovare un metodo certo per consentire al calcolatore di individuare sempre quale bit rappresenta il segno, indipendentemente dalla lunghezza del modulo del numero binario. Ci viene in aiuto il fatto che la dimensione minima della memoria sia di 8 bit. Utilizzando un numero fisso di cifre è possibile assegnare una posizione fissa al bit del segno, che solitamente viene fatto corrispondere al msb (il bit più significativo del byte). I bit compresi fra il segno e il valore assoluto del numero, se necessario, vengono riempiti con dei leading zero.
Per semplificare la spiegazione immaginiamo di lavorare con computer ideali che possono utilizzare un numero fisso di cifre, anche diverso da 8.
esempio
Se scegliamo di utilizzare 4 cifre per rappresentare i valori assoluti, occorre inserire degli 0 davanti ai numeri che hanno meno di 4 cifre.
Quindi per 510, 910 e 210 abbiamo:
La soluzione proposta pone un limite massimo ai valori che possono essere rappresentati.
Pur trattandosi di un metodo semplice e intuitivo per l’uomo, nella pratica la rappresentazione in modulo e segno ha un uso concreto molto limitato perché il bit del segno è di fatto disgiunto (separato) dal resto della rappresentazione. Questo significa che durante i calcoli il bit del segno deve essere trattato a parte, necessitando quindi di circuiti specifici dedicati e/o di software più complessi per riuscire a realizzare automaticamente le operazioni aritmetiche (addizione e sottrazione).
ApprofondiMENTO
IL SEGNO HA PROBLEMI DI “PESO”
Applicando le normali regole di addizione alla rappresentazione in modulo e segno si ha che provando a sommare, per esempio, i numeri + 1 e – 1 si ottiene come risultato – 2 invece di 0. Considerando 4 bit abbiamo la seguente addizione.
|
|
|
12 |
|
|
|
0 |
0 |
0 |
12 |
+ |
|
1 |
0 |
0 |
12 |
= |
|
1 |
0 |
1 |
02 |
Questo accade perché eseguendo la somma algebrica si assume che i bit del segno abbiano un peso binario esattamente come i bit del modulo, ma in realtà il bit del segno, nella rappresentazione MS, non dovrebbe avere peso.
La rappresentazione in complemento a 2
Nel metodo del complemento a 2 (CA2) ai numeri positivi viene semplicemente anteposto un bit di valore 0 che rappresenta il segno +.
I numeri negativi invece vengono ottenuti applicando il seguente algoritmo.
Algoritmo di conversione in complemento a 2.
1. Scrivere il numero di partenza comprensivo del bit del segno;
2. invertire tutte le cifre del numero (complemento a 1, che può essere abbreviato CA1);
3. sommare 1 al numero ottenuto (complemento a 2).
esempio
Con una rappresentazione a 5 bit il numero +12 si scrive: + 1210 = 01100CA2
Il numero –1210 si ottiene applicando l’algoritmo, partendo da +1210, nel modo seguente:
1. 011002
2. 10011CA1
3.|
1 |
0 |
0 |
1 |
1CA1 |
+ |
|
12 |
= |
||||
|
1 |
0 |
1 |
0 |
0CA1 |
da cui otteniamo: – 1210 = 11100CA2
Le caratteristiche della rappresentazione in complemento a 2 la rendono particolarmente vantaggiosa, anche dal punto di vista tecnologico, rispetto alla notazione in modulo e segno perché:
- il passaggio inverso, dal numero negativo alla sua rappresentazione positiva si ottiene applicando lo stesso identico algoritmo;
- il bit più significativo del numero, usato per rappresentare il suo segno non deve essere esaminato separatamente (diversamente da come avviene con la notazione modulo e segno);
- l’elaborazione dei numeri può quindi avvenire mediante circuiti più semplici;
- le addizioni e le sottrazioni si eseguono effettuando sempre un’addizione perché il circuito sommatore, eseguendo una somma algebrica, determina automaticamente il segno del risultato.
esempio
Partiamo dal numero –1210 = 10100CA2 e, applicando l’algoritmo, otteniamo il numero +1210:
1. 101002
2. 01011CA1
3.|
0 |
1 |
0 |
1 |
1CA1 |
+ |
|
12 |
= |
||||
|
0 |
1 |
1 |
0 |
0CA2 |
da cui otteniamo: + 1210 = 01100CA2
esempio
Calcoliamo la differenza + 510 – 1010
Per prima cosa convertiamo i due numeri in complemento a due, considerando che servono almeno 5 bit per rappresentare –1010 in CA2.
Quindi abbiamo:
+ 510 = 00101CA2
– 1010 = 10110CA2
Impostiamo il calcolo della differenza come somma algebrica e lo eseguiamo in colonna:
|
0 |
0 |
1 |
0 |
12 |
+ |
| 1 | 0 | 1 | 1 |
02 |
= |
|
1 |
1 |
0 |
1 |
12 |
da cui otteniamo: 11011CA2 = – 510
Il metodo del complemento a 2 utilizza un numero fisso di cifre per scrivere i numeri, quindi è possibile che in alcuni casi si verifichi un overflow.
esempio
Sommiamo algebricamente, in complemento a 2, i numeri + 710 e + 310 utilizzando per la rappresentazione 3 cifre più il bit del segno.
Applicando l’algoritmo di conversione in complemento a 2 otteniamo:
+ 710 = 0111CA2
+ 310 = 0011CA2
La somma algebrica è:
+ 710 + 310 = 0111CA2 + 0011CA2
|
12 |
12 |
12 |
|
|
|
0 |
1 |
1 |
12 |
+ |
| 0 | 0 | 1 |
12 |
= |
|
1 |
0 |
1 |
02 |
Il risultato dovrebbe essere: + 1010 = 01010CA2 e necessiterebbe di un numero di cifre superiore per essere rappresentato (4 più il bit del segno), invece il risultato che otteniamo è: 1010CA2 = – 610
Si è verificato un overflow.
I sistemi informatici devono tenere conto della possibilità che si verifichi l’overflow, perché in caso di overflow, l’operazione aritmetica non è realizzabile e il sistema deve restituire errore.
Esiste una regola per stabilire l’attendibilità del risultato di un’operazione aritmetica o il verificarsi di una condizione di overflow:
1. se i due numeri sommati hanno segno opposto, l’overflow non si verifica e la somma algebrica va sicuramente a buon fine;
2. se i due numeri considerati hanno lo stesso segno, l’overflow potrebbe verificarsi.
Per capire se effettivamente si verifica l’overflow, occorre controllare i due riporti più a sinistra, cioè quello che entra nel bit del segno e quello che ne esce , se i due riporti sono:
- uguali: l’overflow non si verifica;
- diversi: l’overflow si verifica.
riporti diversi = overflow ▶
| 02 |
12 |
12 |
12 |
|
|
|
0 |
1 |
1 |
12 |
+ |
|
| 0 | 0 | 1 |
12 |
= |
|
| 0 |
1 |
0 |
1 |
02 |
ApprofondiMENTO
IL SEGNO NON HA PROBLEMI DI “PESO”
Applicando le normali regole di addizione alla notazione in complemento a 2 si ha che provando a sommare, per esempio, i numeri + 1 e – 1 si ottiene il risultato corretto, cioè 0. Per esempio con 4 bit si ottiene il codice dello zero e l’1 più a sinistra viene perso nell’overflow, ottenendo il risultato corretto.
| 12 |
12 |
12 |
12 |
|
|
|
0 |
1 |
1 |
12 |
+ |
|
| 1 | 1 | 1 |
12 |
= |
|
| 1 |
0 |
0 |
0 |
02 |
La rappresentazione in complemento a 2, meno intuitiva per gli esseri umani, assegna un peso (nell’esempio 27) al bit del segno consentendo di trattarlo come gli altri bit e semplificando notevolmente le operazioni matematiche all’interno dei calcolatori.
La rappresentazione dei numeri reali
la virgola fissa
Nella rappresentazione in ▶ virgola fissa viene riservato un numero fisso di bit per la parte intera e un numero fisso di bit per la parte decimale. In questo modo la virgola non si muove.
| Parte intera | Parte decimale |
Per esempio se usiamo 3 bit per la parte intera e 2 bit per la parte decimale è possibile rappresentare numeri come:
| 011.012 | 101.112 | 000.102 |
Per conoscere il numero corrispondente in base 10 è sufficiente usare il metodo della griglia, estendendolo alle potenze negative.
esempio
Per il numero 011.012 compiliamo la seguente griglia.
| 0 | 1 | 1 | 0 | 1 |
| 22 | 21 | 20 | 2-1 | 2-2 |
Abbiamo quindi che:
011.012 =
= 1 × 2–2 + 0 × 2–1 + 1 × 20 + 1 × 21 + 0 × 22 =
= 1 × 1/22 + 0 × 1/21 + 1 × 1 + 1 × 2 + 0 × 4 =
= 1 × 1/4 + 0 × 1/2 + 1+ 2+ 0 = 1 × 0.25 + 0 × 0.5 + 3 = 0.25 + 0 + 3 = 3.2510
Una volta effettuata la scelta su come utilizzare i 7 bit, non sarà più possibile usarli per rappresentare intervalli di numeri differenti.
LA VIRGOLA MOBILE
Rendendo la virgola mobile all’interno dei 7 bit, permettendole quindi di posizionarsi in modo dinamico, l’utilizzo dei bit diventa più efficiente.
La rappresentazione in ▶ virgola mobile, come quella in virgola fissa, utilizza un numero fisso di bit per rappresentare i numeri, attribuendo, però, un significato diverso ai bit che in questo caso rappresentano la mantissa e l’esponente usati nella ▶ notazione scientifica (non la parte intera e decimale del numero).
| Mantissa | Esponente |
La notazione scientifica stabilisce che tutti i numeri in base 10 possono essere rappresentati nella forma:
Usando la notazione scientifica per esempio il numero 0,000072342 può essere scritto:
0.000072342 = 7.2342 × 10–5
Ne consegue che la posizione della virgola, in questa notazione, non è fissa, ma può variare in base ai valori che si decide di far assumere alla mantissa e all’esponente.
La notazione esponenziale, che deriva da quella scientifica, lascia sottintesa la base del sistema di numerazione e sostituisce il per 10 elevato a con una E seguita dall’esponente a cui elevare il numero 10. Quindi il numero del precedente esempio diventa:
7.2342 × 10–5 = 7.2342E–5
esempio
Il numero 0.000000000000003 (14 zeri dopo la virgola) si può scrivere nella forma 3E–15.
Il numero 123 000 000 000 000 (12 zeri) si può scrivere nella forma 1.23E+14.
Esiste anche una notazione normalizzata in cui il numero in virgola mobile viene scritto con una mantissa sempre minore di 1. Se consideriamo il secondo numero del precedente esempio otteniamo:
0.123E + 15 con 0 ≤ m < 1
La base della notazione scientifica (o di quella esponenziale) può essere qualunque, non necessariamente 10. I computer lavorano in base 2 perciò anche la notazione scientifica che essi implementano utilizza la base binaria. Per la base 10 il segno del numero viene rappresentato da un simbolo + o – inserito davanti alla mantissa; per la base 2 è necessario prevedere un ulteriore bit dedicato al segno.
In base allo standard IEEE 754, nei computer i numeri reali occupano 32 bit e nella rappresentazione in virgola mobile la suddivisione è la seguente:
Il valore del numero si ricava dalla formula:
(– 1)segno × 2esponente × mantissa
nella quale:
- il bit del segno (che si riferisce alla mantissa e quindi è il segno del numero rappresentato) vale 0 per i numeri positivi e 1 per i numeri negativi;
- la base di numerazione è binaria;
- l’esponente, nei suoi 8 bit, può rappresentare numeri sia positivi sia negativi;
- la mantissa è un numero binario sempre positivo.
Lo sapevi che
IEEE è l’acronimo di Institute of Electrical and Electronic Engineers, che significa Istituto degli ingegneri elettrici ed elettronici. Si tratta di una grande organizzazione mondiale che, nel corso degli anni, ha sviluppato numerosi standard, anche in ambito informatico.
ApprofondiMENTO
L’UNDERFLOW
I numeri reali che non possono essere rappresentati in una memoria non sono solo quelli periodici o quelli che necessitando di troppi bit generano un overflow.
Nella rappresentazione in virgola mobile anche i numeri molto vicini allo zero non possono essere rappresentati a causa del numero finito di bit. Anche nell’intervallo tra un numero rappresentabile e il suo successivo esistono infiniti numeri reali che non possono essere rappresentati.
Clic!
Tecnologie informatiche per il primo biennio