1 INTRODUZIONE ALLA LOGICA
1 INTRODUZIONE ALLA LOGICA
La logica è lo studio del ragionamento che, partendo da alcune premesse, consente di arrivare a determinate conclusioni.
Come la matematica, anche la logica dispone di un proprio linguaggio per esprimere i concetti e gli argomenti studiati. In matematica si usano i numeri, le variabili, gli operatori aritmetici e le espressioni; nella logica si usano le proposizioni semplici, i connettivi logici e le proposizioni composte.
Partiamo quindi dalla definizione della proposizione logica più elementare.
Una proposizione semplice è una qualunque frase, vera o falsa, nell’universo di riferimento.
Questa importante definizione ci fornisce numerose informazioni.
Innanzitutto la logica non studia tutte le frasi, ma considera unicamente le ▶ proposizioni, cioè quelle frasi che sono sempre, sicuramente, o vere, o false.
Per esempio, la frase «2 è un numero pari» può essere considerata, perché si tratta di una proposizione logica vera.
Quando diciamo che una proposizione logica è vera, oppure è falsa, stiamo dando alla frase un valore di verità che indicheremo con vero (V) oppure falso (F).
Il valore di verità di una frase potrebbe anche cambiare in base alle circostanze, ma una proposizione non può mai essere contemporaneamente sia vera sia falsa.
esempio
Se ci soffermiamo a riflettere sull’esempio precedente ci viene, però, un dubbio, attraverso quale finestra dobbiamo guardare? La risposta è: quella che viene indicata dall’universo al quale facciamo riferimento.
Studiando la logica infatti, come sappiamo dalla definizione di proposizione semplice, è importante stabilire un universo al quale fare riferimento.
esempio
«Si diventa maggiorenni a 18 anni»
La proposizione è vera se consideriamo come universo oggi, in Italia, ma fino al 1975 nel nostro paese si diventava maggiorenni a 21 anni; senza contare il fatto che, in altri paesi, la legge stabilisce la maggiore età diversamente.
Nel momento in cui viene fissato l’universo di riferimento (oggi, in Italia), la frase dell’esempio diventa sicuramente vera e quindi diventa una proposizione.
Consideriamo, invece, la frase «1 + 1 = 10», nell’universo decimale è una proposizione falsa ma nell’universo binario è vera. In ogni caso, fissato l’universo di riferimento (sistema decimale oppure binario), la frase considerata è una proposizione logica.
E le frasi che non sono proposizioni? Le frasi che non rientrano nella definizione di proposizione non vengono studiate dalla logica.
Sicuramente non sono proposizioni logiche le frasi né vere né false, come:
«Come stai?» «Torna qui!» «L’informatica è bella»
Se una frase è una domanda, un’affermazione imperativa oppure esprime un’opinione, sicuramente non può trattarsi di una proposizione, perché non è possibile stabilire se è vera oppure falsa.
Al contrario, frasi come le seguenti sono proposizioni logiche, anche se possono sembrare strane:
«La Luna è il satellite della Terra» «Le galline hanno quattro zampe»
Se prendiamo come universo di riferimento il nostro pianeta, la prima proposizione è vera, mentre la seconda è falsa.
Nel linguaggio della logica le proposizioni semplici vengono indicate utilizzando le lettere minuscole dell’alfabeto. Per esempio:
p: «Oggi splende il sole»
q: «La luce è spenta»
prova tu
- una qualunque frase, vera o falsa.
- una qualunque frase, vera o falsa, in un universo di riferimento.
- un universo di riferimento di una qualunque frase, vera o falsa.
I connettivi logici
In matematica è possibile scrivere «2 + 3 = 5», per esprimere il concetto che se si uniscono il numero 2 e il numero 3 utilizzando il +, allora si ottiene un altro numero, il 5, che rappresenta la loro composizione.
Nella logica esiste un’astrazione analoga, in base alla quale utilizzando i connettivi logici è possibile collegare fra loro le proposizioni semplici, ottenendo proposizioni composte. I connettivi logici principali sono:
- ▶ negazione non;
- ▶ congiunzione e;
- ▶ disgiunzione o inclusiva;
- ▶ disgiunzione o esclusiva.
La negazione “non”
Data la proposizione p, la sua negazione è non p e si indica con ¬ p.
Il valore di verità di ¬ p dipende dal valore di verità della proposizione p di partenza che può essere o vera o falsa.
esempio
Data la proposizione semplice:
p: «Oggi piove» la sua negazione è la proposizione composta:
¬ p: «Oggi non piove»
Per stabilire il valore di verità di p basta guardare fuori dalla finestra e constatare quale tra le seguenti possibilità si è verificata.

|

|
|
p: «Oggi piove» è vero ¬ p: «Oggi non piove» è falso |
p: «Oggi piove» è falso ¬ p: «Oggi non piove» è vero |
Possiamo riassumere tutti i casi che si possono verificare scrivendo una tabella di verità.
La tabella di verità è uno strumento che consente di determinare il valore logico di una proposizione a partire dalla proposizione semplice e dal connettivo logico.
| colonna che contiene tutti i valori di verità che può assumere la proposizione semplice di partenza p | p | ¬ p | colonna che contiene tutti i valori di verità che la negazione ¬ p, assume in funzione del valore di p |
| V | F | ||
| F | V |
La negazione è un connettivo logico unario perché opera su una sola proposizione.
Gli altri connettivi logici che analizzaremo, operano invece su due proposizioni e per questo motivo vengono detti connettivi logici binari.
La congiunzione “e”
Date le proposizioni p e q, la loro congiunzione è p e q e si indica con p q.
Il valore di verità di p ^ q dipende dai valori di verità delle proposizioni p e q di partenza che possono essere, ciascuna, o vera o falsa.
esempio
Date le proposizioni semplici: p: «Oggi piove», q: «Marco ha l’ombrello» la loro congiunzione è la proposizione composta:
p ^ q: «Oggi piove e Marco ha l’ombrello»
Per stabilire il valore di verità di p e di q basta guardare fuori dalla finestra e constatare quale tra le seguenti possibilità si è verificata:
«Oggi piove» e «Marco ha l’ombrello»
«Oggi piove» e «Marco non ha l’ombrello»
«Oggi non piove» e «Marco ha l’ombrello»
«Oggi non piove» e «Marco non ha l’ombrello»
- Se guardando dalla finestra vediamo che sta piovendo e che Marco ha l’ombrello, allora la proposizione composta p ^ q: «Oggi piove e Marco ha l’ombrello» è vera.
- Se sta piovendo, ma Marco si sta bagnando perché è senza ombrello, allora la proposizione composta p ^ q: «Oggi piove e Marco ha l’ombrello» è falsa.
- Se non sta piovendo, sia che Marco abbia l’ombrello, sia che non ce l’abbia, la proposizione composta p ^ q: «Oggi piove e Marco ha l’ombrello» non afferma il vero perché non piove e quindi è falsa.
| colonne in cui sono indicate tutte le possibili combinazioni di valori di verità che possono essere assunti dalle proposizioni p e q | p | q | p ∧ q | colonna che contiene tutti i valori di verità che assume p Λ q, in funzione dei valori di p e di q
|
| V | V | V | ||
| V | F | F | ||
| F | V | F | ||
| F | F | F |
prova tu
- La negazione è un connettivo logico binario.
- V F
- Il simbolo della congiunzione è ^.
- V F
La disgiunzione “o” inclusiva
Date le proposizioni p e q, la loro disgiunzione inclusiva è p o q e si indica con p ∨ q.
Il valore di verità di p q dipende dai valori di verità delle proposizioni p e q di partenza che possono essere, ciascuna, o vera o falsa.
esempio
Date le proposizioni semplici dell’esempio precedente la loro disgiunzione inclusiva è la proposizione composta:
p ∨ q: «Oggi piove o Marco ha l’ombrello»
Come per la congiunzione, per stabilire il valore di verità di p e di q basta guardare fuori dalla finestra e constatare quale tra le seguenti possibilità si è verificata:
«Oggi piove» o «Marco ha l’ombrello»
«Oggi piove» o «Marco non ha l’ombrello»
«Oggi non piove» o «Marco ha l’ombrello»
«Oggi non piove» o «Marco non ha l’ombrello»
- La proposizione composta p ∨ q: «Oggi piove o Marco ha l’ombrello» è vera se si verifica almeno una delle due condizioni descritte dalle proposizioni semplici. Quindi, basta che piova e automaticamente la proposizione composta diventa vera.
- Analogamente, è sufficiente che Marco abbia l’ombrello perché la proposizione composta sia vera.
- L’unico caso in cui la proposizione composta p ∨ q: «Oggi piove o Marco ha l’ombrello» è falsa è quello in cui, guardando dalla finestra, si constata che non sta piovendo e inoltre Marco non ha l’ombrello.
Possiamo riassumere tutti i casi che si possono verificare scrivendo la tabella di verità per la disgiunzione inclusiva.
| colonne in cui sono indicate tutte le possibili combinazioni di valori di verità che possono essere assunti dalle proposizioni p e q
|
p | q | p ∨ q | colonna che contiene tutti i valori di verità che assume p ∨ q, in funzione dei valori di p e di q
|
| V | V | V | ||
| V | F | V | ||
| F | V | V | ||
| F | F | F |
La disgiunzione inclusiva è falsa solo quando le proposizioni che la compongono sono entrambe false. In tutti gli altri casi, è vera.
La disgiunzione inclusiva si chiama così perché include la possibilità che entrambe le proposizioni semplici p e q si possano verificare contemporaneamente. Esistono però casi in cui questa possibilità non può essere contemplata.
Lo sapevi che
Il termine latino vel, che significava “o” con senso inclusivo, ha forse prestato l’iniziale al simbolo per rappresentare la disgiunzione inclusiva.
La disgiunzione o esclusiva
Nel linguaggio comune usiamo il connettivo o in due modi diversi, spesso senza rendercene conto; infatti, può avere un significato:
- inclusivo (latino vel): quando include la possibilità che le ipotesi (p e q) possano essere vere entrambe nello stesso momento;
- esclusivo (latino aut): quando esclude la possibilità che le ipotesi (p e q) possano essere vere entrambe nello stesso momento e pertanto il verificarsi delle due ipotesi è strettamente alternativa.
esempio
Consideriamo le seguenti proposizioni composte.
«Marco guarda la televisione o mangia i pop corn»
La proposizione composta è vera se Marco guarda la televisione oppure se mangia i pop corn ed è falsa se non fa nessuna delle due attività.
Nulla esclude che Marco possa fare le due cose contemporaneamente: se guarda la tv mangiando i pop corn, la proposizione resta vera.
«Andrea va a lavorare in treno o in automobile»
La proposizione composta è vera se Andrea va a lavorare in treno o se va a lavorare con l’automobile. La proposizione è falsa se Andrea non usa né il treno, né l’automobile.
Il verificarsi di uno dei due casi esclude il contemporaneo verificarsi dell’altro! Se Andrea va a lavorare in treno non è possibile che usi contemporaneamente l’automobile, e viceversa.
Nella logica i due tipi di o vengono considerati separatamente prendendo rispettivamente il nome di ▶ o inclusivo (OR) e ▶ o esclusivo (XOR).
Date le proposizioni p e q, la loro disgiunzione esclusiva è p o q e si indica con p ⩒ q.
Il valore di verità di p ⩒ q dipende dai valori di verità delle proposizioni p e q di partenza che possono essere, ciascuna, o vera o falsa.
esempio
Date le proposizioni semplici: p: «Andrea va a lavorare in treno»,
q: «Andrea va a lavorare in automobile» la loro disgiunzione esclusiva è:
p ⩒ q: «Andrea va a lavorare in treno o in automobile»
Ancora una volta, per stabilire il valore di verità di p e di q basta guardare
che cosa sta facendo Andrea e constatare quale tra le seguenti possibilità
si è verificata:
«Andrea va a lavorare in treno» (e quindi non in automobile)
«Andrea va a lavorare in automobile» (e quindi non in treno)
«Andrea non va a lavorare né in treno né in automobile» (magari va a piedi!)
L’unica ipotesi alla quale non è consentito verificarsi è «Andrea va a lavorare
in treno e in automobile» (è impossibile) e pertanto risulta falsa.
Possiamo riassumere tutti i casi che si possono verificare scrivendo la tabella di verità della disgiunzione esclusiva.
| colonne in cui sono indicate tutte le possibili combinazioni di valori di verità che possono essere assunti dalle proposizioni p e q
|
p | q | p ⩒ q | colonna che contiene tutti i valori di verità che assume p ⩒ q, in funzione dei valori di p e di q
|
| V | V | F | ||
| V | F | V | ||
| F | V | V | ||
| F | F | F |
Le proposizioni composte e le tabelle di verità
Come abbiamo visto, applicando i connettivi logici alle proposizioni semplici, si ottengono delle proposizioni composte. È possibile applicare i connettivi logici anche alle proposizioni composte ottenendo altre proposizioni composte, via via sempre più articolate.
In generale una proposizione composta è una frase formata da più proposizioni, legate fra loro da connettivi logici.
esempio
Date le proposizioni semplici: p: «Roberta ascolta la musica», q: «Roberta canta» è possibile ottenere, fra le altre, la proposizione composta:
(p ∨ ¬ p) ∧ ¬ q
che potrebbe essere letta «Roberta ascolta la musica o non la ascolta, e non canta».
Fino a questo momento dare un significato alle proposizioni (semplici o composte) è stato utile per comprendere meglio come lavora la logica. Da questo punto in avanti abbandoneremo le frasi e useremo solo la notazione letterale delle proposizioni.
Come le proposizioni semplici, anche quelle composte possiedono un proprio valore di verità, vero (V) oppure falso (F), che dipende dal valore di verità delle proposizioni che le costituiscono.
La ricerca del valore di verità delle proposizioni composte è oggetto di studio della logica e prende il nome di calcolo proposizionale.
Per stabilire i valori di verità delle proposizioni composte, si ricorre alle tabelle di verità.
La costruzione delle tabelle di verità
La tabella di verità di una proposizione composta si costruisce per passi successivi, come quando si risolve un’espressione algebrica.
- Passo 1: si osserva la proposizione composta e si determinano le proposizioni semplici contenute al suo interno (N). Ciascuna proposizione, anche se compare più volte, deve essere conteggiata una volta sola.
- Passo 2: si utilizza la formula R = 2N per ottenere il numero di righe (R) della tabella di verità.
- Passo 3: si disegna una tabella di R righe inserendo nelle prime N colonne le proposizioni semplici.
- Passo 4: nella prima colonna si inseriscono delle V nella prima metà delle righe e delle F nella seconda metà. Le successive colonne riferite alle proposizioni semplici vanno riempite tenendo conto della colonna precedente: vicino alle V (della colonna precedente) si inseriscono metà V e metà F e si fa la stessa cosa per le F. Si continua per tutte le proposizioni semplici presenti nella tabella.
- Passo 5: se nella proposizione composta ci sono delle proposizioni semplici negate, si completano le colonne corrispondenti determinando i valori di verità a partire dalle proposizioni semplici.
- Passo 6: osservando la proposizione composta di partenza, e tenendo conto delle colonne già ottenute, si determina quale sotto-proposizione composta considerare per scrivere la nuova colonna.
- Passo 7: si ripete il passo 6 fino a determinare i valori logici della colonna che si riferisce all’intera proposizione composta di partenza.
esempio
Determiniamo i valori di verità della proposizione composta: (p ∨ ¬ p) ∧ ¬ q
Passo 1: le proposizioni semplici sono 2 (p e q); anche se p compare due volte, quindi N = 2
Passo 2: R = 2N = 22 = 4
Passo 3: la tabella ha R = 4 righe e N = 2 proposizioni (colonne verdi).
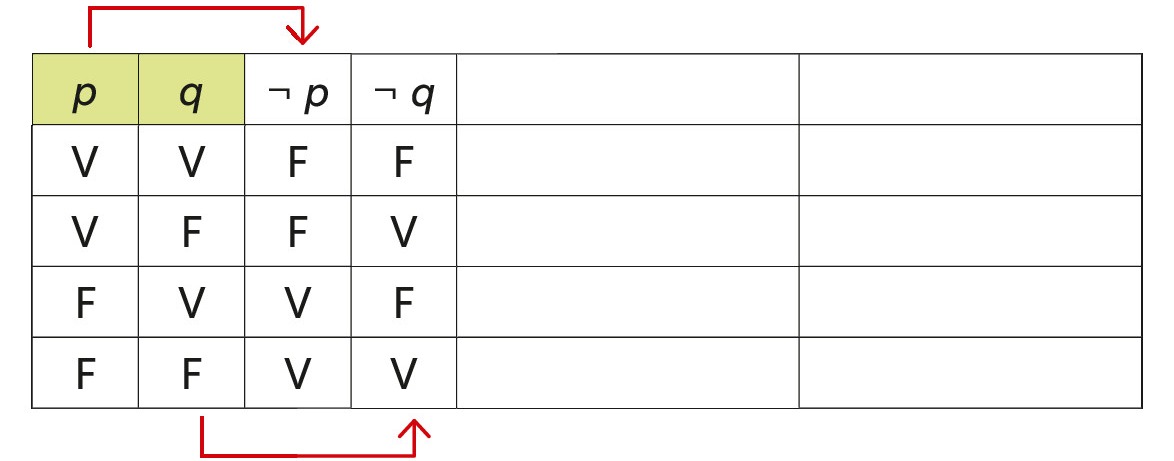
Passo 4: inseriamo le V e le F a partire dalla prima colonna, per tutte le proposizioni semplici (colonne verdi), come mostrato in figura.

Passo 5: per determinare ¬ p guardiamo la colonna p e scriviamo il valore di verità opposto (dove p è vera, scriviamo che ¬ p è falsa e viceversa). Procediamo allo stesso modo per determinare ¬ q.
Passo 6: consideriamo la sotto-proposizione contenuta nella parentesi, cioè (p ∨ ¬ p). Questa sotto-proposizione ci dice che il connettivo logico da utilizzare è la o inclusiva e che le colonne da considerare sono quella di p e quella di ¬ p.
Passo 7: resta da mettere in relazione con il connettivo logico e la colonna di (p ∨ ¬ p) e quella di ¬ q.
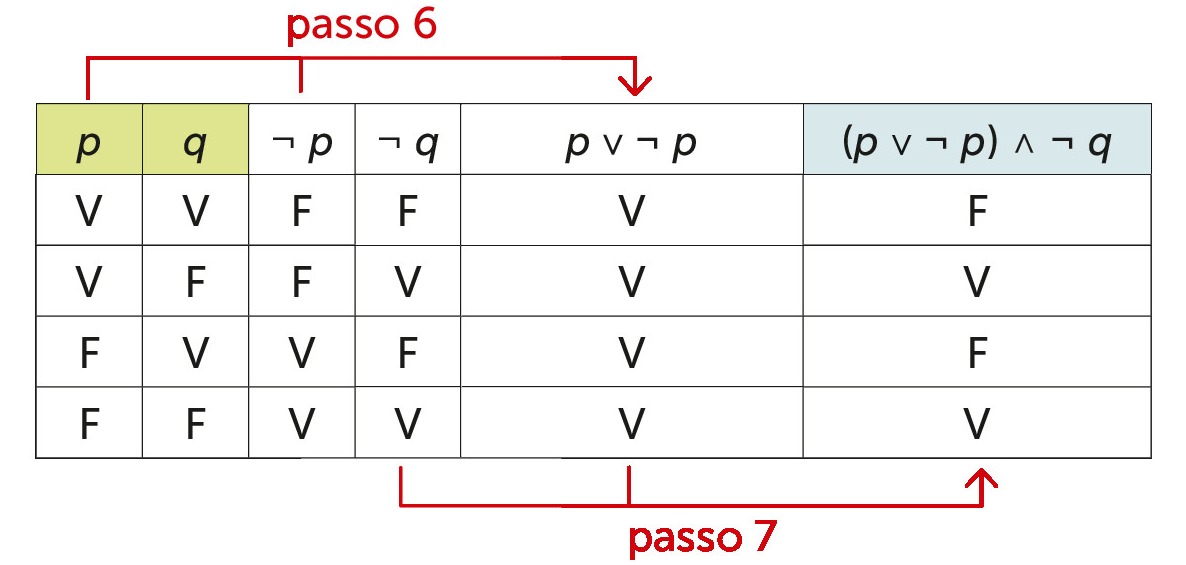
La tabella di verità elenca tutte le ipotesi (nelle colonne in verde), cioè tutti i possibili modi in cui le proposizioni semplici possono essere verificate.
Con i calcoli proposizionali, che permettono di ottenere le colonne intermedie (colonne in bianco), la tabella di verità consente di conoscere, per ciascuna ipotesi, il corrispondente valore di verità della proposizione composta (colonna in azzurro).
Quando la proposizione composta è formata da più di due proposizioni semplici, la tabella di verità aumenta il numero delle righe perché aumenta il numero delle possibili combinazioni iniziali.
esempio
Determiniamo i valori di verità della proposizione composta: p ∧ (q ⩒ r)
Passo 1: le proposizioni semplici sono p, q e r, quindi:
N = 3
Passo 2: R = 2N = 23 = 8
Passo 3: la tabella ha R = 8 righe e N = 3 proposizioni.
Passo 4: inseriamo le V e le F a partire dalla prima colonna, per tutte le proposizioni semplici, come mostrato in figura.
Nell’ultima colonna (verde) le V e le F risultano sempre alternate.
| p | q | r | ||
| V | V | V | ||
| V | V | F | ||
| V | F | V | ||
| V | F | F | ||
| F | V | V | ||
| F | V | F | ||
| F | F | V | ||
| F | F | F |
Passo 5: si salta perché non ci sono proposizioni negate.
Passo 6: la prima sotto-proposizione da considerare è quella fra parentesi, cioè (q ⩒ r).
Passo 7: resta da considerare la proposizione composta di partenza.
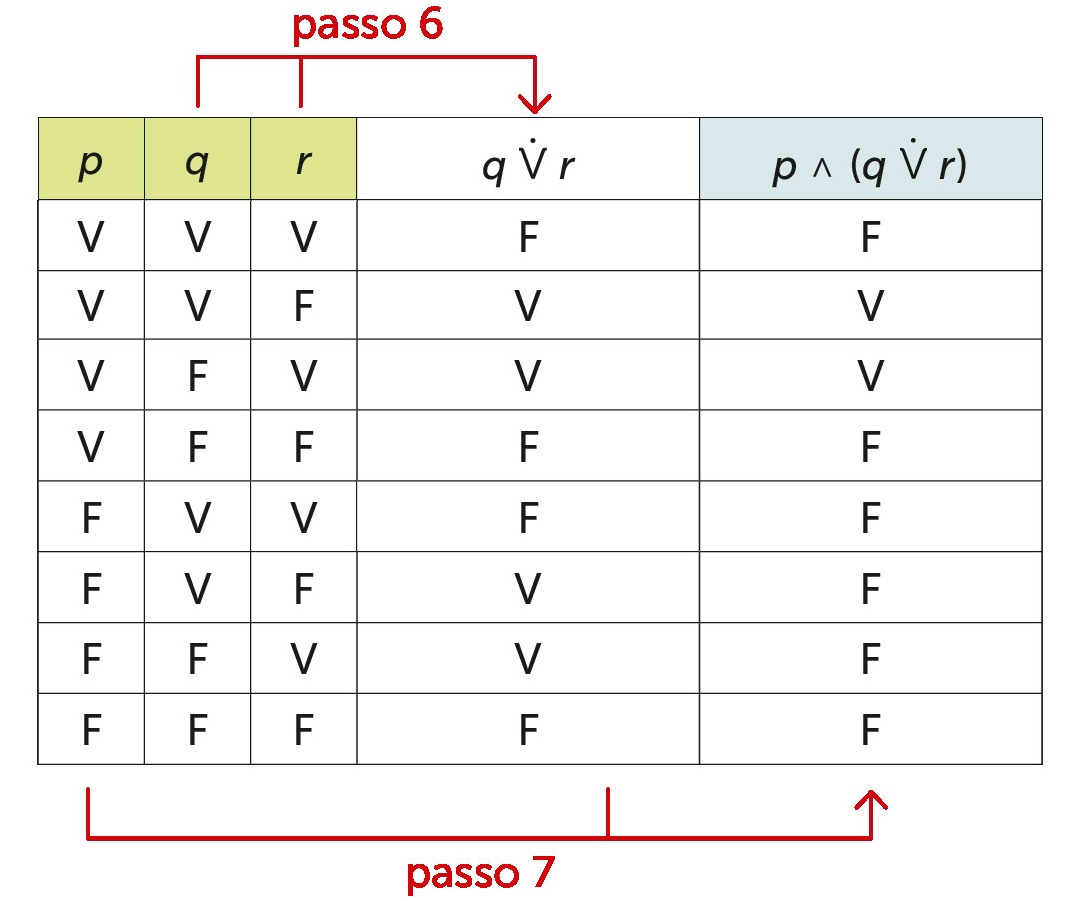
Il calcolo proposizionale può essere effettuato compilando le tabelle di verità o individuando direttamente i valori di verità delle proposizioni composte. Basta sostituire i valori di verità delle proposizioni semplici in quella composta.
Se consideriamo la tabella di verità dell’esempio precedente essa ci informa che nell’ipotesi di: p = F • q = F • r = V la proposizione composta vale F.
| p | q | r | q ⩒ r | p ∧ (q ⩒ r) |
| V | V | V | F | F |
| V | V | F | V | V |
| V | F | V | V | V |
| V | F | F | F | F |
| F | V | V | F | F |
| F | V | F | V | F |
| F | F | V | V | F |
| F | F | F | F | F |
Lo stesso risultato può essere ottenuto attraverso la sostituzione diretta nella proposizione composta:
p ∧ (q ⩒ r) = F ∧ (F ⩒ V) = F ∧ (V) = F ∧ V = F
prova tu
Costruisci la tabella di verità delle proposizioni.
- (¬ a ∧ a) ∨ (¬ b ∧ b)
- (a ∧ b ∧ c) ∨ (a ∧ b ∧ ¬ c)
- (¬ a ∧ b ∧ c) ⩒ (¬ a ∧ ¬ b ∧ c)
Le proposizioni logicamente equivalenti
Due proposizioni sono logicamente equivalenti se partendo dalle stesse ipotesi (colonne in verde) si arriva per entrambe alle stesse conclusioni (colonne in azzurro).
Per capire se due proposizioni sono logicamente equivalenti occorre costruire le tabelle di verità di entrambe e verificare se sono uguali.
Per poter considerare uguali due tabelle di verità di due proposizioni diverse basta che siano identiche solo le colonne delle ipotesi (verdi) e quelle delle conclusioni (azzurre). Il contenuto delle colonne intermedie (bianche) non è rilevante ai fini dell’uguaglianza fra le tabelle.
Per comodità, spesso due tabelle vengono costruite all’interno di un’unica tabella complessiva: in questo modo le colonne delle ipotesi (verdi) vengono scritte una volta sola e sicuramente coincideranno, mentre l’uguaglianza delle colonne delle conclusioni (azzurre) diventa l’unica da verificare.
esempio
Vogliamo dimostrare che: p ∧ (q ∨ r) = (p ∧ q) ∧ (p ∧ r)
Dobbiamo costruire una tabella complessiva, all’interno della quale sia possibile individuare sia la tabella di verità della prima proposizione (indicata in rosso) sia la tabella di verità della seconda proposizione (indicata in blu).
Poiché le colonne delle ipotesi (verdi) coincidono e le colonne delle conclusioni (azzurre) sono identiche fra loro, si può affermare che le due tabelle di verità sono uguali e che quindi le proposizioni composte da cui esse derivano siano logicamente equivalenti.
A conclusione di questo argomento, vale la pena di sottolineare che i colori verde, azzurro e bianco utilizzati nella trattazione non costituiscono una convenzione universalmente riconosciuta. Le tabelle di verità, infatti, normalmente non hanno colori specifici, nella nostra trattazione abbiamo deciso di inserirli per aiutare la memorizzazione dei concetti.
- Le colonne identificate con il colore verde contenevano tutte le possibili combinazioni di valori di verità delle proposizioni semplici di partenza (ipotesi).
- Le colonne identificate con il colore azzurro contenevano tutti i valori di verità assunti dalle proposizioni composte di “arrivo”, in funzione dei valori delle proposizioni semplici di “partenza”.
- Le colonne identificate con il colore bianco contenevano gli eventuali passaggi intermedi che non sono sempre identici, ma dipendono dalla strategia adottata per il calcolo proposizionale.
ApprofondiMENTO
I CONNETTIVI LOGICI E GLI INSIEMI
In matematica, l’intersezione fra due insiemi P e Q viene definita come l’insieme degli elementi che appartengono al primo insieme e al secondo insieme.
L’unione U tra due insiemi P e Q viene invece definita come l’insieme degli elementi che appartengono al primo insieme o al secondo insieme.
Esiste una corrispondenza tra i connettivi logici e e le operazioni sugli insiemi e U e i loro simboli ce lo ricordano!
SCHEDA CLIL
Necessary conditions vs sufficient conditions
When speaking about logic, statements may be true or false and their value may affect the value of other statements. We often refer to such statements as “conditions”.
The logical operation that bounds the first statement with the second statement is called “implication”, or “logical consequence”.
When statement A implies statement B, we can say that if A is true, then B comes true, too.
In this case, we say that statement A is a sufficient condition for statement B. It means that it’s enough to have A true to imply that B is also true.
On the other hand: when A is false, and such condition implies that B is false, too, we say that statement A is a necessary condition for B. If B is true, A must be true. But if A is true, B can be any value (true o false). There are statements A that can be both necessary and sufficient for B. When it happens, we say that A is a necessary and sufficient condition for B. The vice versa also happens. We say “if and only if A happens, then B happens, too”.
In computer science: “if A then B” states that A is a sufficient condition for B to happen.
Clic!
Tecnologie informatiche per il primo biennio